Big O in JavaScript
Imagine we have multiple implementations for the same function, how do we figure out which one's best? And here BigO comes to use
So what is Big O?
-> Big O notation is a mathematical representation that describes the upper bound or worst-case scenario of an algorithm's time complexity or space complexity in terms of the input size.
For most algorithms, the goal is to design and optimize them to have the best possible Big O complexity, ensuring efficient and scalable performance for larger datasets. However, it's important to note that Big O notation only describes the upper bound and the actual performance might vary depending on the specific implementation and hardware considerations.
Why is Big O important?
-> Knowing Big O helps and facilitates developers being aware of the "efficiency of an algorithm" so they can code applications with good performance.
At times, our priority may shift towards conserving memory rather than minimizing time or iterations, resulting in a trade-off between time and space efficiency. This balance is evident not only in saving read time versus disk space but also when comparing relational (normalized) and non-relational (denormalized) databases.
Comparing the complexities of various Big O notations reveals their different scaling behaviours. Each notation represents how an algorithm's time or space requirements change concerning the input size. By examining these complexities, we gain insight into the efficiency and scalability of algorithms under different circumstances.
-> How do we derive the BigO of an algorithm? Let us understand this with an example. Here T is the time complexity of BigO

when we are choosing the best algorithm we have two questions on our mind depending upon the case.
how fast does it run? (time complexity)
how much space in memory does it occupy? (space complexity)
so now we shall deep dive into these matters.
Time complexity
Time complexity describes the amount of time an algorithm takes to run as a function of the input size "n." It tells us how the algorithm's running time increases with larger inputs. In Big O notation, we ignore constant factors and lower-order terms, focusing only on the dominant term that grows the fastest.
Here are some common time complexities:
O(1): Constant Time - The algorithm takes a constant amount of time regardless of the input size.
O(log n): Logarithmic Time - The running time increases logarithmically with the input size.
O(n): Linear Time - The running time increases linearly with the input size.
O(n log n): Linearithmic Time - The running time increases in between linear and logarithmic growth.
O(n^2): Quadratic Time - The running time increases quadratically with the input size.
O(n^k): Polynomial Time - The running time increases with an exponent "k" of the input size "n."
O(2^n): Exponential Time - The running time grows exponentially with the input size, often very slow and impractical for large inputs.
Space Complexity
Space complexity describes the amount of memory an algorithm uses as a function of the input size "n." Similar to time complexity, we focus on the dominant term that grows the fastest and ignores constant factors and lower-order terms.
The space complexity of an algorithm can be different from its time complexity. Here are some examples:
O(1): Constant Space - The algorithm uses a fixed amount of memory regardless of the input size.
O(n): Linear Space - The algorithm's memory usage increases linearly with the input size.
O(n^2): Quadratic Space - The algorithm's memory usage increases quadratically with the input size.
It's important to analyze the time and space complexity of algorithms to understand their efficiency and suitability for different problem sizes. Generally, algorithms with lower time and space complexity are more efficient and preferred for larger input sizes. However, sometimes trade-offs are necessary based on the specific requirements and constraints of a problem.
-> Using BigOs to compare algorithms
Now that we understand the complexities we can compare different BigO's time complexities.
the image below shows descending order from fast to slow of a few commonly used BigO notations.

-> Let us consider a problem and compare BigO notations of its different solutions, and the problem is to add n natural numbers.
solution 1 is to use a for loop
function sumUp(n) {
let result =0
for( let i = 1; i<=n; i++) {
result +=1;
}
return result
}

so solution 1 's BigO notation is a linear function whose graph is shown above.

the function has 4 statements,
the Statement 1,3,4 i.e. every statement except for the "for loop" runs once irrespective of n
where as the for loop runs once for n=1 , twice for n=2 and n times for n=n
hence its BigO notation is O(f(n))
solution 2 is to use a mathematical formula to add n natural numbers.
which is (n/2)*(n+1)
function sumUp(n) {
return (n/2) * (n+1);
}

so solution 2's BigO notation is a constant function whose graph is shown above.

the algorithm used in solution 2 has one statement which runs only once irrespective of the value of n. Hence it is a constant function whose BigO is represented as O(f(1)).
-> we denote BigO as O(f(n)) where f(n) could be
1)linear : f(n)=n
2) quadratic : f(n)=n^2
3) constant : f(n) = 1
or it could be something entirely different like a logarithm, exponential or factorial function.
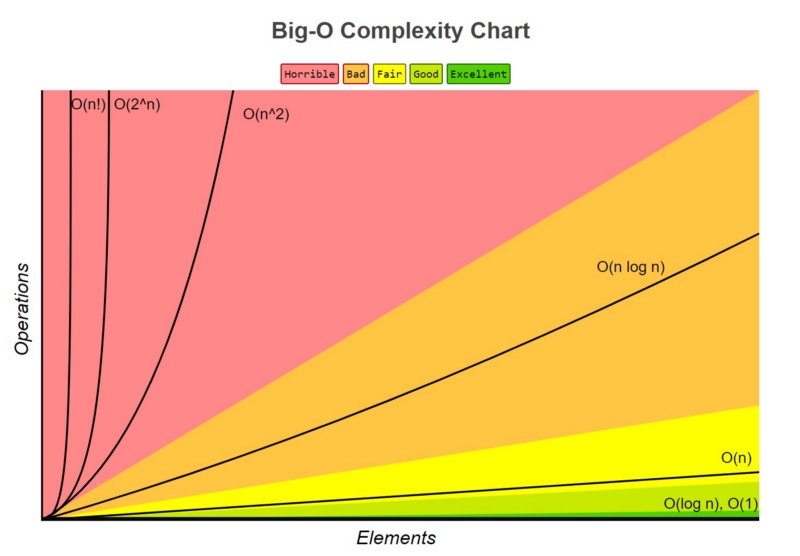
Here are examples of different types of BigOs we may come across while writing algorithms↓
A linear time complexity algorithm (O(n)) in JavaScript typically involves traversing through each element of an array or performing a task for each item in the input. Let's look at an example of linear time complexity in JavaScript.
Example: Finding the sum of elements in an array.function findSum(arr) { let sum = 0; for (let i = 0; i < arr.length; i++) { sum += arr[i]; } return sum; } const numbers = [1, 2, 3, 4, 5]; console.log(findSum(numbers)); // Output: 15Quadratic time complexity (O(n^2)\*)* is commonly seen in algorithms that involve nested loops. It means that the algorithm's running time increases quadratically with the input size. Let's look at an example of quadratic time complexity in JavaScript.
Example: Finding all pairs of elements in an array.
function printAllPairs(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length; j++) {
console.log(arr[i], arr[j]);
}
}
}
const numbers = [1, 2, 3];
printAllPairs(numbers); // Output : When we run the code with the numbers array containing three elements, it will produce the following output:
1 1
1 2
1 3
2 1
2 2
2 3
3 1
3 2
3 3
Since there are two nested loops, the total number of iterations becomes quadratic. Thus, the time complexity of this algorithm is O(n^2), where 'n' is the number of elements in the array.
- Constant time complexity algorithm (O(1)) is one where the execution time or memory usage remains constant, regardless of the input size. Let's look at an example of constant time complexity in JavaScript.
Example: Finding the sum and product of two numbers.
const a = 5;
const b = 10;
const sum = a + b; // Constant time addition
const product = a * b; // Constant time multiplication
console.log(sum); // Output: 15
console.log(product); // Output: 50
This is the most efficient scenario where the algorithm's performance does not vary with the input size, making it highly desirable for many programming tasks.
- sLogarithmic time complexity O(log(n)) involves dividing the input data into smaller chunks or segments to perform operations more efficiently. Let's look at an example of logarithmic time complexity in JavaScript.
Example: binary search algorithm is a classic example of a logarithmic time complexity algorithm.
Binary search is used to find a specific element in a sorted array by repeatedly dividing the array in half and narrowing down the search range until the target element is found or deemed absent.
function binarySearch(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
const midValue = arr[mid];
if (midValue === target) {
return mid; // Found the target element at index 'mid'
} else if (midValue < target) {
left = mid + 1; // Target element is in the right half
} else {
right = mid - 1; // Target element is in the left half
}
}
return -1; // Target element not found
}
const numbers = [1, 3, 5, 7, 9, 11, 13, 15];
const target = 9;
console.log(binarySearch(numbers, target)); // Output: 4 (index of the target element)
Exponential time complexity (O(b^n)) an algorithm is said to have an exponential time complexity if its runtime grows exponentially with the size of the input. The general representation of exponential time complexity in Big O notation is O(b^n), where 'b' is any constant greater than 1, and 'n' is the size of the input.
This means that for every additional element in the input, the algorithm's runtime increases exponentially, leading to a rapidly growing number of operations.
Exponential time complexity is generally considered inefficient and can quickly become impractical for larger input sizes. Algorithms with exponential time complexity are often associated with brute-force approaches or algorithms that involve exploring all possible combinations or permutations. Let's look at an example of exponential time complexity (O(2^n)) in JavaScript.
Example: An example of an algorithm with an exponential time complexity of O(2^n) in JavaScript is the recursive Fibonacci sequence calculation. The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding ones. The recursive implementation of the Fibonacci sequence has an exponential time complexity because it calculates the same values repeatedly, leading to a large number of redundant calculations.
Here's the recursive implementation of the Fibonacci sequence with O(2^n) time complexity:
codefunction fibonacciRecursive(n) {
if (n <= 0) return 0;
if (n === 1) return 1;
return fibonacciRecursive(n - 1) + fibonacciRecursive(n - 2);
}
// Example usage
console.log(fibonacciRecursive(5)); // Output: 5
console.log(fibonacciRecursive(10)); // Output: 55
In this implementation, to find the nth Fibonacci number, the function makes two recursive calls to calculate the (n-1)th and (n-2)th Fibonacci numbers, and those recursive calls, in turn, make more recursive calls, leading to an exponential growth in the number of function calls.
Factorial time complexity (O(n!)) an algorithm with O(n!) time complexity means that the number of operations required to solve the problem grows at a rate proportional to 'n!'. The factorial function is defined as the product of all positive integers less than or equal to 'n', denoted by 'n!'. Mathematically, it can be expressed as:
n! = n (n - 1) (n - 2) ... 2 * 1
An algorithm with O(n!) time complexity often involves trying out all possible permutations or combinations of a given set of 'n' elements, resulting in a large number of operations. Let's look at an example of factorial time complexity in JavaScript.
Example: An example of an algorithm with a time complexity of O(n!) is the brute-force solution for generating all possible permutations of a set of 'n' elements.
Let's see an implementation of generating all permutations of a given array using a recursive approach:function permuteHelper(array, currentIndex, result) { if (currentIndex === array.length - 1) { result.push([...array]); return; } for (let i = currentIndex; i < array.length; i++) { // Swap elements to create a new permutation [array[currentIndex], array[i]] = [array[i], array[currentIndex]]; // Recursively generate permutations for the remaining elements permuteHelper(array, currentIndex + 1, result); // Restore the array to its original state (backtrack) [array[currentIndex], array[i]] = [array[i], array[currentIndex]]; } } function permute(array) { const result = []; permuteHelper(array, 0, result); return result; } // Example usage const inputArray = [1, 2, 3]; console.log(permute(inputArray));
In this example, we have an array of 'n' elements, and the permute function generates all possible permutations of this array. The permuteHelper function is a recursive helper function that uses backtracking to create permutations. For each element at the current index, it swaps with all the elements following it, recursively generates permutations for the remaining elements, and then restores the array to its original state (backtrack) to explore other possibilities.
Algorithms with O(n!) time complexity are generally avoided for larger 'n', and more efficient algorithms or optimizations are sought to solve the problem in a reasonable amount of time.
It is essential to analyze and optimize algorithms carefully to avoid this level of time complexity whenever possible.
now let us go through BigO notations for different types of sorts.
-> BigO notations for different types of sorts in JavaScript
Bubble sort
function bubbleSort(arr) {
for (let i = arr.length; i > 0; i--) {
for (let j = 0; j < i - 1; j++) {
if (arr[j] > arr[j + 1]) {
let temp = arr[j]
arr[j] = arr[j + 1]
arr[j + 1] = temp
}
}
}
return arr
}
The time complexity of this code is O(n^2).
Selection sort
function selectionSort(arr) {
for (let i = 0; i < arr.length; i++) {
let lowest = i
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[lowest]) {
lowest = j
}
}
if (i !== lowest) {
let temp = arr[i]
arr[i] = arr[lowest]
arr[lowest] = temp
}
}
return arr
}
The time complexity of this code is O(n^2).
Insertion sort
function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let currentVal = arr[i]
for (var j = i - 1; j >= 0 && arr[j] > currentVal; j--) {
arr[j + 1] = arr[j]
}
arr[j + 1] = currentVal
}
return arr
}
The time complexity of this code is O(n^2).
Quick sort
this is an example of nlog(n) complexity
function pivot(arr, start = 0, end = arr.length + 1) {
let pivot = arr[start]
let swapIdx = start
function swap(array, i, j) {
let temp = array[i]
array[i] = array[j]
array[j] = temp
}
for (let i = start + 1; i < arr.length; i++) {
if (pivot > arr[i]) {
swapIdx++
swap(arr, swapIdx, i)
}
}
swap(arr, start, swapIdx)
return swapIdx
}
function quickSort(arr, left = 0, right = arr.length - 1) {
if (left < right) {
let pivotIndex = pivot(arr, left, right)
quickSort(arr, left, pivotIndex - 1)
quickSort(arr, pivotIndex + 1, right)
}
return arr
}
The time complexity of this code is O(n log(n)).

->The main lesson from this is that Big O notation serves as a mathematical tool to estimate the resources used by an algorithm. In practice, the actual results may vary, but it is still wise to aim for reducing the complexity of our algorithms as much as possible unless we encounter a specific scenario where we are confident in our approach.